In this last post about reduced paths, I’m going to work through the details of one of the most useful results in wild topology. Writing this post helped me work out my own way of proving this result and hopefully will help bring together some ideas from the literature in a unique way in a way that is helpful to folks trying to learn about some of the techniques of the field.
Unique Reduced Path Theorem: If  is a one-dimensional Hausdorff space, then every path
is a one-dimensional Hausdorff space, then every path ![\alpha:[0,1]\to X](https://s0.wp.com/latex.php?latex=%5Calpha%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) is path-homotopic to a reduced path
is path-homotopic to a reduced path ![\beta:[0,1]\to X](https://s0.wp.com/latex.php?latex=%5Cbeta%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) that is unique up to reparameterization. Moreover, the homotopy between
that is unique up to reparameterization. Moreover, the homotopy between  and
and  has image in
has image in 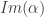 .
.
Although stated a little differently, this was basically proven in [2]. The contemporary version appears in [1]. This theorem changed the game for me. Instead of using inverse limits all of the time, this allowed me to understand and prove things using order theory and unique reduced representatives.
First, it might be helpful to give more explanation of the statement itself.
- What does one-dimensional mean? Actually, you can use any of the three standard notions of dimension (Lebesgue covering, small inductive, or large inductive) and this theorem would still be true. Generally, Lebesgue covering dimension is the typical choice.
- Recall from Part I that a path
![\beta:[0,1]\to X](https://s0.wp.com/latex.php?latex=%5Cbeta%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) being reduced means that
being reduced means that  has no null-homotopic subloops, i.e. there is no
has no null-homotopic subloops, i.e. there is no ![[a,b]\subseteq [0,1]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D%5Csubseteq+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that ![\beta|_{[a,b]}](https://s0.wp.com/latex.php?latex=%5Cbeta%7C_%7B%5Ba%2Cb%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a null-homotopic loop.
is a null-homotopic loop.
- What does “unique up to reparameterization” mean? A path
![\beta:[a,b]\to X](https://s0.wp.com/latex.php?latex=%5Cbeta%3A%5Ba%2Cb%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) is a reparameterization of a path
is a reparameterization of a path ![\gamma:[c,d]\to X](https://s0.wp.com/latex.php?latex=%5Cgamma%3A%5Bc%2Cd%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) if there is an increasing homeomorphism
if there is an increasing homeomorphism ![h:[c,d]\to [a,b]](https://s0.wp.com/latex.php?latex=h%3A%5Bc%2Cd%5D%5Cto+%5Ba%2Cb%5D&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  . I use the notation
. I use the notation 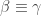 when this occurs. Reparameterization is an equivalence relation on the set of paths in a space. So “unique up to reparameterization” means that if
when this occurs. Reparameterization is an equivalence relation on the set of paths in a space. So “unique up to reparameterization” means that if  and
and  are homotopic reduced paths in a 1-dim. space, then
are homotopic reduced paths in a 1-dim. space, then  .
.
- The last statement of the theorem implies that deforming
 to its reduced representative only requires deleting portions of
to its reduced representative only requires deleting portions of  . As a special case, if
. As a special case, if  is a null-homotopic loop, then it contracts in its own image.
is a null-homotopic loop, then it contracts in its own image.
One-dimensional Peano continua
We need to dive into some terminology and “well-known” results from General Topology here. I’ve used these terms and results before but here’s a reminder:
An arc (respectively, simple closed curve) in a space  is a subspace of
is a subspace of  that is homeomorphic to
that is homeomorphic to ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) (respectively,
(respectively, 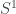 ). If
). If ![h:[0,1]\to X](https://s0.wp.com/latex.php?latex=h%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) is an embedding onto the arc
is an embedding onto the arc ![A=h([0,1])](https://s0.wp.com/latex.php?latex=A%3Dh%28%5B0%2C1%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) , we call
, we call  and
and 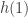 the endpoints of the arc. Notice that an “arc” is technically not the same thing as an embedding
the endpoints of the arc. Notice that an “arc” is technically not the same thing as an embedding ![[0,1]\to X](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) . Rather an arc is the image of such an embedding with the subspace topology.
. Rather an arc is the image of such an embedding with the subspace topology.
A space  is uniquely arcwise connected, if given any distinct
is uniquely arcwise connected, if given any distinct  , there is a unique arc
, there is a unique arc  with endpoints
with endpoints  and
and  .
.
A Peano continuum is a connected, locally path-connected compact metric space. The Hahn-Mazurkiewicz Theorem says that a space  is a Peano continuum if and only if
is a Peano continuum if and only if  is Hausdorff and there exists a continuous surjection
is Hausdorff and there exists a continuous surjection ![[0,1]\to X](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) .
.
A dendrite is a Peano continuum that has no simple closed curves. I go into some of the theory of dendrites in this old post on shape injectivity. In particular, I mention a well-known structure theorem, which says that a dendrite  is homeomorphic to an inverse limit
is homeomorphic to an inverse limit  of trees
of trees 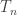 where
where  is
is 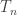 with a single edge attached and each bonding map
with a single edge attached and each bonding map 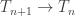 collapses that edge to the vertex at which it is attached. In Part II of the Shape Injectivity Post, we used this structure theorem to prove that dendrites are contractible.
collapses that edge to the vertex at which it is attached. In Part II of the Shape Injectivity Post, we used this structure theorem to prove that dendrites are contractible.
To put these old posts to work here’s a theorem that I mentioned at the end of Part II.
Inverse Limit Representation Theorem [3, Theorem 1]: Every one-dimensional path-connected compact metric space  can be written as an inverse limit
can be written as an inverse limit 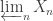 of finite graphs
of finite graphs 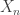 .
.
In fact, this is improved a bit in [4] where it is shown that it is possible to improve a given inverse system to ensure that all bonding maps  map
map 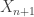 surjectively and simplicially onto some finite subdivision of
surjectively and simplicially onto some finite subdivision of 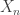 .
.
Dendrite Factorization Lemma
The next lemma is at the heart of why we can do so much in wild one-dimensional spaces like the earring space, Menger Cube, and higher-dimensional constructions that start with one-dimensional spaces, e.g. the Harmonic Archipelago. The proof for a general space  is the same as that for loops where
is the same as that for loops where 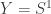 so I went ahead and wrote out the general proof.
so I went ahead and wrote out the general proof.
Lemma: If  is a one-dimensional Hausdorff space,
is a one-dimensional Hausdorff space,  is a Peano continuum, and
is a Peano continuum, and  is a null-homotopic map based at
is a null-homotopic map based at 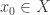 , then
, then  factors through a dendrite, that is, there is a dendrite
factors through a dendrite, that is, there is a dendrite  a map
a map  and a map
and a map  such that
such that  .
.
Proof. Assuming that  is non-constant, notice that
is non-constant, notice that 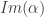 is one-dimensional and Hausdorff (as a subspace of a one-dimensional Hausdorff space that admits a non-constant path). Since
is one-dimensional and Hausdorff (as a subspace of a one-dimensional Hausdorff space that admits a non-constant path). Since 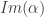 is a Hausdorff continuous image of a Peano continuum, it is a Peano continuum by the Hahn-Mazurkiewicz Theorem. Hence, we may assume that
is a Hausdorff continuous image of a Peano continuum, it is a Peano continuum by the Hahn-Mazurkiewicz Theorem. Hence, we may assume that 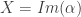 and that
and that  is a Peano continuum.
is a Peano continuum.
Using the Inverse Limit Representation Theorem, write  with bonding maps
with bonding maps  and finite graphs
and finite graphs 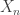 . If
. If  are the projections, we take
are the projections, we take  to be the basepoints in the graphs. Let
to be the basepoints in the graphs. Let  be the universal covering map where
be the universal covering map where 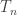 is a tree. As we did in Part II of the Shape Injectivity Post, once we choose basepoints
is a tree. As we did in Part II of the Shape Injectivity Post, once we choose basepoints  , the maps
, the maps 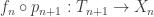 induce unique based maps
induce unique based maps  that give the following inverse system of covering maps.
that give the following inverse system of covering maps.

Since  is null-homotopic in
is null-homotopic in  and each latex
and each latex 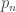 is a Hurewicz fibration, the map
is a Hurewicz fibration, the map  is null-homotopic in the graph
is null-homotopic in the graph 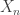 and has a unique lift to a based map
and has a unique lift to a based map  . These based lifts agree with the bonding maps
. These based lifts agree with the bonding maps  and give the inverse system of covering maps you see below. The universal property of inverse limits gives a unique map
and give the inverse system of covering maps you see below. The universal property of inverse limits gives a unique map 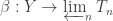 based at
based at  such that.
such that.  . In fact, Hurewicz fibrations are closed under inverse limits so
. In fact, Hurewicz fibrations are closed under inverse limits so  is also a Hurewicz fibration!
is also a Hurewicz fibration!

Let  . Since the inverse limit of trees
. Since the inverse limit of trees  is clearly Hausdorff,
is clearly Hausdorff,  is a Peano continuum. Moreover, I gave a detailed proof in Part I of the Shape Injectivity Post that an inverse limit of trees contains no simple closed curves. Since
is a Peano continuum. Moreover, I gave a detailed proof in Part I of the Shape Injectivity Post that an inverse limit of trees contains no simple closed curves. Since  is a Peano continuum with no simple closed curves, it must be a dendrite! Taking
is a Peano continuum with no simple closed curves, it must be a dendrite! Taking  to be the restriction of
to be the restriction of  to
to  , completes the proof.
, completes the proof. 
We could replace 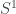 with any Peano continuum in the next Corollary, but I’ll try to keep it focused.
with any Peano continuum in the next Corollary, but I’ll try to keep it focused.
Corollary: Every null-homotopic loop 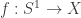 in a one-dimensional Hausdorff space
in a one-dimensional Hausdorff space  contracts in its own image.
contracts in its own image.
Proof. Suppose  is a null-homotopic map. By the previous Lemma, we have
is a null-homotopic map. By the previous Lemma, we have 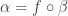 for a map
for a map  and map
and map 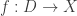 where
where  is a dendrite. Set
is a dendrite. Set 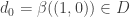 . Since
. Since  is contractible, there is a null-homotopy latex
is contractible, there is a null-homotopy latex ![H:S^1\times [0,1] \to D](https://s0.wp.com/latex.php?latex=H%3AS%5E1%5Ctimes+%5B0%2C1%5D+%5Cto+D&bg=ffffff&fg=333333&s=0&c=20201002) with
with 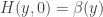 ,
, 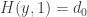 . Now
. Now 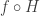 is a null-homotopy of
is a null-homotopy of  .
. 
The null-homotopy  in the last proof is a “free” null-homotopy but since
in the last proof is a “free” null-homotopy but since 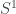 is well-pointed, you could just as easily construct a basepoint-preserving homotopy.
is well-pointed, you could just as easily construct a basepoint-preserving homotopy.
Getting back on track, we’d like to apply the general results in Part II, which says that homotopy classes of paths will have reduced representatives if our space has well-defined transfinite 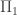 -products. So let’s make sure that happens.
-products. So let’s make sure that happens.
Proposition: Every one-dimensional Hausdorff space has well-defined transfinite 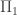 -products.
-products.
Proof. Let  be a one-dimensional Hausdorff space. Suppose
be a one-dimensional Hausdorff space. Suppose ![A\subseteq [0,1]](https://s0.wp.com/latex.php?latex=A%5Csubseteq+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a closed set containing
is a closed set containing  and
and ![\alpha,\beta:[0,1]\to X](https://s0.wp.com/latex.php?latex=%5Calpha%2C%5Cbeta%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) are paths such that
are paths such that  and such that for every connected component
and such that for every connected component  of
of ![[0,1]\backslash A](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Cbackslash+A&bg=ffffff&fg=333333&s=0&c=20201002) , we have
, we have  . We must show that
. We must show that  . For each component
. For each component  of
of ![[0,1]\backslash A](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Cbackslash+A&bg=ffffff&fg=333333&s=0&c=20201002) , the loop
, the loop  is null-homotopic and therefore (by the last Corollary) contracts by a null-homotopy in
is null-homotopic and therefore (by the last Corollary) contracts by a null-homotopy in 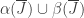 . In particular, there exists an endpoint-relative homotopy
. In particular, there exists an endpoint-relative homotopy ![H_{I}:\overline{J}\times [0,1]\to X](https://s0.wp.com/latex.php?latex=H_%7BI%7D%3A%5Coverline%7BJ%7D%5Ctimes+%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where
We just need to put these all together! Define ![H:[0,1]^2\to X](https://s0.wp.com/latex.php?latex=H%3A%5B0%2C1%5D%5E2%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) by
by
![H(s,t)=\begin{cases} \alpha(s), & \text{ if }s\in A, \\ H_J(s,t), & \text{ if }s\in J\text{ for a component }J\text{ of }[0,1]\backslash A \end{cases}](https://s0.wp.com/latex.php?latex=H%28s%2Ct%29%3D%5Cbegin%7Bcases%7D+%5Calpha%28s%29%2C%C2%A0+%26+%5Ctext%7B+if+%7Ds%5Cin+A%2C+%5C%5C+H_J%28s%2Ct%29%2C+%26+%5Ctext%7B+if+%7Ds%5Cin+J%5Ctext%7B+for+a+component+%7DJ%5Ctext%7B+of+%7D%5B0%2C1%5D%5Cbackslash+A+%5Cend%7Bcases%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Notice that ![H|_{A\times[0,1]}](https://s0.wp.com/latex.php?latex=H%7C_%7BA%5Ctimes%5B0%2C1%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) is the constant homotopy at
is the constant homotopy at  .
.
Checking continuity of

would be considered “routine” for those who make these constructions a lot so sometimes these things are skipped in the literature. But a blog is a good place to lay out the details for those who are still getting used to the proof techniques. So let’s do it!
Fix ![(s,t)\in [0,1]^2](https://s0.wp.com/latex.php?latex=%28s%2Ct%29%5Cin+%5B0%2C1%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) and an open neighborhood
and an open neighborhood  of
of  in
in  . Since each
. Since each 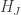 is continuous,
is continuous,  is continuous at
is continuous at 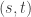 if
if  for some component
for some component  of
of ![[0,1]\backslash A](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Cbackslash+A&bg=ffffff&fg=333333&s=0&c=20201002) . So we may assume
. So we may assume  . Since
. Since  and
and  are continuous at
are continuous at  , there exists
, there exists 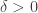 such that
such that ![\alpha([s-\delta,s+\delta])\cup \beta([s-\delta,s+\delta])\subseteq U](https://s0.wp.com/latex.php?latex=%5Calpha%28%5Bs-%5Cdelta%2Cs%2B%5Cdelta%5D%29%5Ccup+%5Cbeta%28%5Bs-%5Cdelta%2Cs%2B%5Cdelta%5D%29%5Csubseteq+U&bg=ffffff&fg=333333&s=0&c=20201002) . We now have
. We now have ![H([([s-\delta,s+\delta]\cap A)\times [0,1])=\alpha([s-\delta,s+\delta]\cap A)\subseteq U](https://s0.wp.com/latex.php?latex=H%28%5B%28%5Bs-%5Cdelta%2Cs%2B%5Cdelta%5D%5Ccap+A%29%5Ctimes+%5B0%2C1%5D%29%3D%5Calpha%28%5Bs-%5Cdelta%2Cs%2B%5Cdelta%5D%5Ccap+A%29%5Csubseteq+U&bg=ffffff&fg=333333&s=0&c=20201002) . If
. If ![J\subseteq [s-\delta,s+\delta]](https://s0.wp.com/latex.php?latex=J%5Csubseteq+%5Bs-%5Cdelta%2Cs%2B%5Cdelta%5D&bg=ffffff&fg=333333&s=0&c=20201002) , then
, then ![H(\overline{J}\times [0,1])=Im(H_J)\subseteq \alpha(\overline{J})\cup\beta(\overline{J})\subseteq U](https://s0.wp.com/latex.php?latex=H%28%5Coverline%7BJ%7D%5Ctimes+%5B0%2C1%5D%29%3DIm%28H_J%29%5Csubseteq+%5Calpha%28%5Coverline%7BJ%7D%29%5Ccup%5Cbeta%28%5Coverline%7BJ%7D%29%5Csubseteq+U&bg=ffffff&fg=333333&s=0&c=20201002) by the definition of
by the definition of  . What remains is to consider components
. What remains is to consider components  having
having  as an endpoint.
as an endpoint.
If  is not an endpoint of a component of
is not an endpoint of a component of ![[0,1]\backslash A](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Cbackslash+A&bg=ffffff&fg=333333&s=0&c=20201002) , then we may find
, then we may find 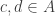 such that
such that ![s\in (c,d)\subseteq [s-\delta,s+\delta]](https://s0.wp.com/latex.php?latex=s%5Cin+%28c%2Cd%29%5Csubseteq+%5Bs-%5Cdelta%2Cs%2B%5Cdelta%5D&bg=ffffff&fg=333333&s=0&c=20201002) . If
. If  is a right endpoint of a component latex
is a right endpoint of a component latex  , then we may choose
, then we may choose  small enough so that
small enough so that ![H((c,s]\times[0,1])=H_J((c,s]\times[0,1])\subseteq U](https://s0.wp.com/latex.php?latex=H%28%28c%2Cs%5D%5Ctimes%5B0%2C1%5D%29%3DH_J%28%28c%2Cs%5D%5Ctimes%5B0%2C1%5D%29%5Csubseteq+U&bg=ffffff&fg=333333&s=0&c=20201002) (by the continuity of
(by the continuity of 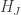 ). Similarly, if
). Similarly, if  is a left endpoint of a component
is a left endpoint of a component 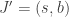 , then we may choose
, then we may choose  small enough so that
small enough so that ![H([s,d)\times[0,1])=H_{J'}([s,d)\times[0,1])\subseteq U](https://s0.wp.com/latex.php?latex=H%28%5Bs%2Cd%29%5Ctimes%5B0%2C1%5D%29%3DH_%7BJ%27%7D%28%5Bs%2Cd%29%5Ctimes%5B0%2C1%5D%29%5Csubseteq+U&bg=ffffff&fg=333333&s=0&c=20201002) . In any case, we can find an open interval
. In any case, we can find an open interval 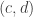 of
of  such that
such that ![H((c,d)\times[0,1])\subseteq U](https://s0.wp.com/latex.php?latex=H%28%28c%2Cd%29%5Ctimes%5B0%2C1%5D%29%5Csubseteq+U&bg=ffffff&fg=333333&s=0&c=20201002) .
. 
The main point of Part II, was to show that every path  in a Hausdorff space with well-defined transfinite
in a Hausdorff space with well-defined transfinite 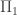 -products is path-homotopic to a reduced path. This path-homotopy was defined by “deleting” null-homotopic subloops on a maximal cancellation and therefore had image in the image of
-products is path-homotopic to a reduced path. This path-homotopy was defined by “deleting” null-homotopic subloops on a maximal cancellation and therefore had image in the image of  . Combining this old stuff with the above proposition, it must be that every path in a one-dimensional Hausdorff space is path-homotopic to a reduced path by a homotopy that takes place in the image of that path itself. This proves the existence portion of the Unique Reduced Path Theorem as well as the last statement about the size of the homotopy required.
. Combining this old stuff with the above proposition, it must be that every path in a one-dimensional Hausdorff space is path-homotopic to a reduced path by a homotopy that takes place in the image of that path itself. This proves the existence portion of the Unique Reduced Path Theorem as well as the last statement about the size of the homotopy required.
Uniqueness of reduced paths in one-dimensional spaces
Dendrites have their infinitely many little fingers all over this content. We’ll need them again to finish the proof of uniqueness.
Lemma: If  is a one-dimensional Hausdorff space and
is a one-dimensional Hausdorff space and ![\alpha,\beta:[0,1]\to X](https://s0.wp.com/latex.php?latex=%5Calpha%2C%5Cbeta%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) are reduced and path-homotopic to each other, then
are reduced and path-homotopic to each other, then  , i.e. there exists an increasing homeomorphism
, i.e. there exists an increasing homeomorphism ![h:[0,1]\to [0,1]](https://s0.wp.com/latex.php?latex=h%3A%5B0%2C1%5D%5Cto+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  .
.
Proof. By replacing  with the image of a homotopy from
with the image of a homotopy from  to
to  , we may assume that
, we may assume that  is a Peano continuum. Now
is a Peano continuum. Now 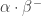 is a null-homotopic loop and so by Dendrite factorization, there exists a dendrite
is a null-homotopic loop and so by Dendrite factorization, there exists a dendrite  , a loop
, a loop ![\gamma:[0,1]\to D](https://s0.wp.com/latex.php?latex=%5Cgamma%3A%5B0%2C1%5D%5Cto+D&bg=ffffff&fg=333333&s=0&c=20201002) , and a map
, and a map 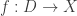 such that
such that  . Write
. Write 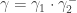 so that
so that  and
and 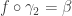 . Let
. Let  and
and  . Recall that dendrites are uniquely arcwise connected and so there is a unique arc
. Recall that dendrites are uniquely arcwise connected and so there is a unique arc  in
in  with endpoints
with endpoints  and
and 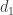 . Now
. Now 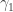 is a path in
is a path in  from
from  to
to 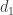 . We check that
. We check that 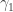 is injective and therefore a parameterization of
is injective and therefore a parameterization of  . If
. If  such that
such that  , then
, then ![(\gamma_1)|_{[a,b]}](https://s0.wp.com/latex.php?latex=%28%5Cgamma_1%29%7C_%7B%5Ba%2Cb%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) would be a loop. Since dendrites are contractible,
would be a loop. Since dendrites are contractible, ![(\gamma_1)|_{[a,b]}](https://s0.wp.com/latex.php?latex=%28%5Cgamma_1%29%7C_%7B%5Ba%2Cb%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a null-homotopic loop. Then
is a null-homotopic loop. Then ![\alpha|_{[a,b]}=f\circ(\gamma_1)|_{[a,b]}](https://s0.wp.com/latex.php?latex=%5Calpha%7C_%7B%5Ba%2Cb%5D%7D%3Df%5Ccirc%28%5Cgamma_1%29%7C_%7B%5Ba%2Cb%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) must also be a null-homotopic loop. However, this violates the assumption that
must also be a null-homotopic loop. However, this violates the assumption that  is reduced. Since
is reduced. Since  is also reduced, applying the same argument to
is also reduced, applying the same argument to 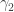 shows that
shows that 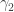 also parameterizes
also parameterizes  . Since both
. Since both ![\gamma_1,\gamma_2:[0,1]\to A](https://s0.wp.com/latex.php?latex=%5Cgamma_1%2C%5Cgamma_2%3A%5B0%2C1%5D%5Cto+A&bg=ffffff&fg=333333&s=0&c=20201002) are homeomorphisms with the same orientation, we consider the increasing homeomorphism
are homeomorphisms with the same orientation, we consider the increasing homeomorphism ![h=\gamma_{2}^{-}\circ\gamma_{1}:[0,1]\to [0,1]](https://s0.wp.com/latex.php?latex=h%3D%5Cgamma_%7B2%7D%5E%7B-%7D%5Ccirc%5Cgamma_%7B1%7D%3A%5B0%2C1%5D%5Cto+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Now
. Now  , which completes the proof.
, which completes the proof.  .
.
What’s the Takeaway?
Imagine you’ve got a based loop ![\alpha:[0,1]\to X](https://s0.wp.com/latex.php?latex=%5Calpha%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) where
where  is the earring space or, more amazingly, the Menger cube. The homotopy class
is the earring space or, more amazingly, the Menger cube. The homotopy class ![[\alpha]](https://s0.wp.com/latex.php?latex=%5B%5Calpha%5D&bg=ffffff&fg=333333&s=0&c=20201002) in the fundamental group is represented by a “tightest” loop
in the fundamental group is represented by a “tightest” loop  that has absolutely no homotopical redundancy. Every point
that has absolutely no homotopical redundancy. Every point  is crucial to that homotopy class and the order in which those points are traced out in
is crucial to that homotopy class and the order in which those points are traced out in  is completely unique.
is completely unique.
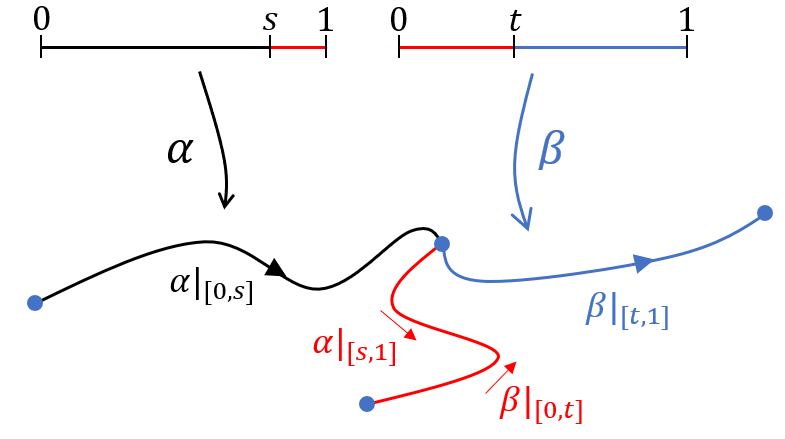
This also tells you about the operation in the fundamental groupoid 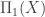 too. Suppose you’ve got two composable path-homotopy classes
too. Suppose you’ve got two composable path-homotopy classes  . Write
. Write ![g=[\alpha]](https://s0.wp.com/latex.php?latex=g%3D%5B%5Calpha%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![h=[\beta]](https://s0.wp.com/latex.php?latex=h%3D%5B%5Cbeta%5D&bg=ffffff&fg=333333&s=0&c=20201002) for reduced paths
for reduced paths  and
and  . Then the product
. Then the product 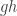 is represented by the concatenation
is represented by the concatenation 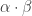 . However,
. However, 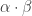 may not be reduced. But, it’s still homotopic to some reduced path
may not be reduced. But, it’s still homotopic to some reduced path  and that reduced representative is obtained by deleting null-homotopic subloops on a maximal cancellation. But wait! There’s only one possible way for this to happen because the entirety of
and that reduced representative is obtained by deleting null-homotopic subloops on a maximal cancellation. But wait! There’s only one possible way for this to happen because the entirety of  and
and  are both reduced. A maximal cancellation of
are both reduced. A maximal cancellation of 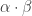 can only contain one interval, which must contain the concatenation point
can only contain one interval, which must contain the concatenation point 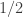 . Hence, there exists
. Hence, there exists  and
and  such that
such that ![\alpha|_{[s,1]}\simeq \beta|_{[0,t]}^{-}](https://s0.wp.com/latex.php?latex=%5Calpha%7C_%7B%5Bs%2C1%5D%7D%5Csimeq+%5Cbeta%7C_%7B%5B0%2Ct%5D%7D%5E%7B-%7D&bg=ffffff&fg=333333&s=0&c=20201002) . There’s more! If a path is reduced, then all of its subpaths are reduced too. Since
. There’s more! If a path is reduced, then all of its subpaths are reduced too. Since ![\alpha|_{[s,1]}](https://s0.wp.com/latex.php?latex=%5Calpha%7C_%7B%5Bs%2C1%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![\beta|_{[0,t]}^{-}](https://s0.wp.com/latex.php?latex=%5Cbeta%7C_%7B%5B0%2Ct%5D%7D%5E%7B-%7D&bg=ffffff&fg=333333&s=0&c=20201002) are homotopic reduced paths, which means they are actually reparameterizations of each other.
are homotopic reduced paths, which means they are actually reparameterizations of each other.
Theorem: Suppose
![\alpha,\beta:[0,1]\to X](https://s0.wp.com/latex.php?latex=%5Calpha%2C%5Cbeta%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002)
are reduced paths in a one-dimensional Hausdorff space satisfying
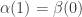
. Then either
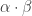
is reduced or there exists unique

and

such that
![\alpha|_{[s,1]}\equiv \beta|_{[t,1]}^{-}](https://s0.wp.com/latex.php?latex=%5Calpha%7C_%7B%5Bs%2C1%5D%7D%5Cequiv+%5Cbeta%7C_%7B%5Bt%2C1%5D%7D%5E%7B-%7D&bg=ffffff&fg=333333&s=0&c=20201002)
and
![\alpha|_{[0,s]}\cdot\beta|_{[t,1]}](https://s0.wp.com/latex.php?latex=%5Calpha%7C_%7B%5B0%2Cs%5D%7D%5Ccdot%5Cbeta%7C_%7B%5Bt%2C1%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
is a reduced path representing
![[\alpha][\beta]](https://s0.wp.com/latex.php?latex=%5B%5Calpha%5D%5B%5Cbeta%5D&bg=ffffff&fg=333333&s=0&c=20201002)
.
[1] J.W. Cannon, G.R. Conner, On the fundamental groups of one-dimensional spaces, Topology Appl. 153 (2006) 2648–2672.
[2] M.L. Curtis, M.K. Fort, Jr., The fundamental group of one-dimensional spaces, Proc. Amer. Math. Soc. 10 (1959) 140–148.
[3] Mardešic, S., Segal, J.,  –Mappings onto polyhedra. Trans. Am. Math. Soc. 109, 146–164 (1963)
–Mappings onto polyhedra. Trans. Am. Math. Soc. 109, 146–164 (1963)
[4] Rogers, J.W. Jr., Inverse limits on graphs and monotone mappings. Trans. Am. Math. Soc. 176, 215–225 (1973)
for totally ordered sets
and
provided there exists an order isomorphism between them. The concatenation of totally ordered sets
and
is denoted
and is the disjoint union
under the obvious order. If
is a collection of totally ordered sets, indexed by a totally ordered set
, then the concatenation
is the totally ordered set which is the disjoint union
under the natural order.
and
there exists a maximal interval
such that
and
is
-pure. We can therefore write
where each
is a maximal nonempty interval in
for which
is
-pure, and the totally ordered set
is unique up to
. This gives rise to a decomposition of the word
as
where
. This decomposition we call the p-decomposition and write
to express that the p-decomposition of
is the concatenation
. We let
denote the totally ordered set
, which is well-defined up to
. Of course,
. As an example, one can consider the word
and
where
.
is a p-chunk of the word
provided there exists some interval
such that
(we may indeed write
). Thus a p-chunk of a word is a subword which respects the p-decomposition. Given an interval
we write
for the p-chunk
. An
-pure p-chunk of a word
will clearly either be
or will be one of the
. Given
we will let
denote the set of all p-chunks of
. Note that this set might be uncountable (if
then consider the p-chunks associated with the Dedekind cuts). Given a subset
we let
denote the generated subgroup
. One can prove that this subgroup is closed under taking p-chunks of elements.
there similarly exists a decomposition of
into maximal nonempty intervals
where
is
-pure. Thus we obtain a decomposition, which we again call the p-decomposition and use the same notation
and again write
to identify the p-index.
with
and
is finite then we have
, and similarly for a word
. This fact that the
class is preserved under deleting finitely many elements of the p-index and then reducing provides the motivation for the essential idea in constructing the isomorphism. We recount the idea now.
we will say that a subset
is close in
if for every infinite interval
we have
. For example, if
is finite then every subset of
, including
, is close in
. If
then any infinite subset
is close in
. If
then every dense subset of
will be close in
. If
and
are totally ordered sets and
and
are each close then we call an order isomorphism
a close order isomorphism (abbreviated coi) from
to
.
from
to
defines a correspondence (not necessarily one-to-one) between the intervals of
and those in
: given interval
we obtain interval
. For an interval
we define
similarly. Many nice properties hold for this correspondence; for instance, we have
is a subinterval of
and there exist (possibly empty) finite subintervals
such that
.
and
and
is a coi from
to
then we write
and call such a triple a coi triple. A collection
of coi triples is coherent if for any choice of
, intervals
and
, and
such that
, intervals
and
, and
such that
.
and
. Thus, great care must be taken in producing a coherent collection of coi triples. For a coherent example, one can take
and let
be the unique order isomorphism between
and
. Of course, one needs to check that the appropriate conditions hold in order to conclude that
is coherent. As a hint in this easy example, one can see that if
are intervals and
and either of
or
is finite, then both are finite and
. If at least one of
or
is infinite then both must be infinite and in fact
implies
and the desired equality once again holds. One cannot have
if either of
or
is infinite (by considering the order type), and if either of
or
is finite we again see that
. The check for intervals in
is comparable.
and
denote the respective quotient maps. A coherent collection
of coi triples induces an isomorphism
.
which is plentiful enough that
and
. That these natural maps (extending
) are well-defined requires some effort, since a word
might decompose in many distinct ways as a finitary concatenation of elements in
, and coherence is essential to the argument. Once these homomorphisms are in hand, it is easier to see that they descend to homomorphisms
and
and that these homomorphisms are inverse to each other.