Inverse limits of planar Peano continua are not always planar

Posted on November 5, 2025 by Jeremy Brazas

Recently, I ran into a situation where I had an inverse sequence of *planar Peano continua. I wondered naively if the limit of such a sequence always had to be planar. It turns out the answer is no, even in the one-dimensional case, but I don’t this fact is particularly obvious. After a literature search I found a really nice example that I can’t help but share.

*A Peano continuum is a connected, locally connected, metrizable space (equivalently, a continuous image of [0,1]) and a space X is planar if there exists a topological embedding X\to \mathbb{R}^2. For instance, the Sierpinski Carpet is a planar Peano continuum.

Kuratowski’s Theorem [3] says that a connected graph G is planar if and only if it contains a topological copy of K_{3,3} or K_5 (see below).

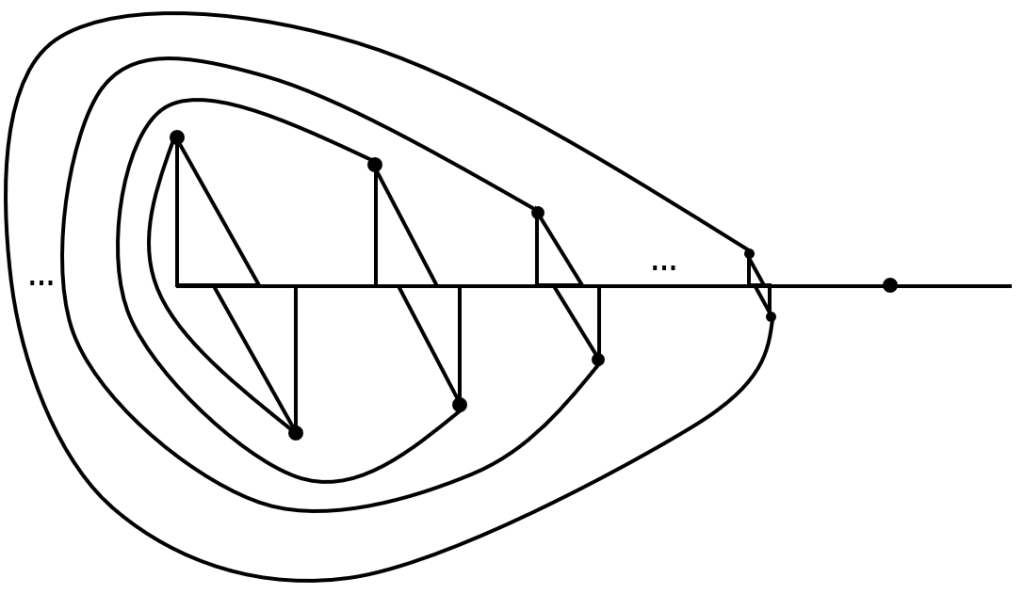
Let’s use an infinite null-sequence of copies of K_{3,3} but without the large overarching arc. We’re going to connect these and make them limit to a point. We’ll also extend the connecting line a little past the limit point. We end up with the following space L_1. Kuratowski actually mentioned this space in [5] and suggested it’s potential importance.

Let’s see why L_1 is not planar. Let’s call the long diagonal edges in the each partial copy of K_{3,3} the “crossing edges” since these are involved in a crossing-over. The sequence of crossing edges is null in the sense that the diameter of these edges approaches 0. We could take finitely many crossing edges and push them over the left end. But we can’t move all of them over the left end or we wind up with a space that is not homeomorphic to L_1. Similarly, because we have extended the connecting line a little past the limit point on the right, we can only push finitely many of the connecting edges over the right side of the space. Hence, any embedding into \mathbb{R}^2 would have infinitely many crossings somewhere and we’d have a contradiction.

However, if we delete all but finitely many of the partial copies of L_1, we would end up with a finite planar graph:

A finite approximation to L_1 with only finitely many partial copies of K_{3,3}.

This finite approximation graph is planar since there are only finitely many crossing edges and we can move all of them over the left side. Here’s a planar embedding of this finite approximation.

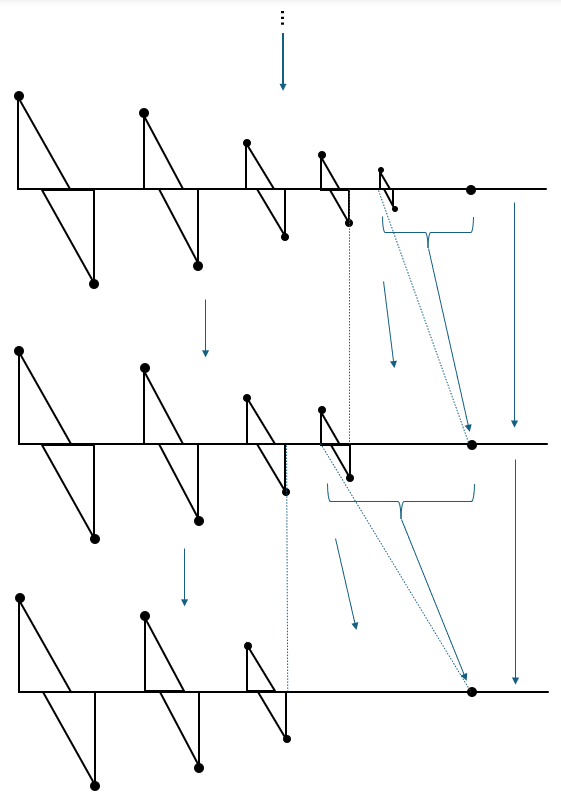
These finite approximations (where we keep only finitely many partial copies of K_{3,3} can be put into an inverse system whose limit is homeomorphic to L_1. To do this correctly, you need to define the bonding maps carefully. Let X_n\subseteq L_1 be the finite graph consisting of the entire horizontal arc and n of the partial copies of K_{3,3}, let’s call them G_1,G_2,G_3,\dots . To ensure that the subspaces G_n shrinking toward the limit point on the arc as n\to \infty, we need to define the bonding map f_{n+1,n}:X_{n+1}\to X_n to map G_{n+1} and the arc connecting G_{n+1} to the limit point to the limit point. We map G_k to itself by the identity for all 1\leq k\leq n, including the arcs connecting them. The arc connecting G_{n+1} and G_{n} we stretch out and map onto the arc connecting G_n and the limit point in X_n. I’ve illustrated the maps f_{5,4} and f_{4,3} below.

It’s not too hard to see that L_1\cong \varprojlim_{n}(X_n,f_{n+1,n}). Hence, we have the following answer to my original naive question: The inverse limit of one-dimensional planar Peano continua need not be planar.

You can also perform a similar construction with K_5. In particular, the following space, which we’ll call L_2 is built out of partial copies of K_5 in an analogous way.

I learned about these spaces in the paper [1]. It also taught me about the following remarkable statement proved by S. Claytor in 1937.

Claytor’s Theorem [2]: A Peano continuum embeds in \mathbb{R}^2 if and only it does not contain a homeomorphic copy of K_{3,3}, K_5, L_1, or L_2.

This completely characterizes the planarity of Peano continua in a way that directly extends Kuratowski’s Theorem! Amazing!

References

[1] R. Ayala; M. Chávez; A. Quintero, On the planarity of Peano generalized continua: An extension of a theorem of S. Claytor, Colloquium Mathematicae 75 (1998) no. 2, 175-181.

[2] S. Claytor, Peanian continua not imbeddable in a spherical surface, Ann. of Math. 38 (1937), 631–646.

[3] K. Kuratowski, Sur le probl`eme des courbes gauches en topologie, Fund. Math. 15 (1930), 271–283.

Posted in Cech expansion, General topology, Inverse Limits, one-dimensional spaces, Peano continuum | Tagged , , , , , | Leave a comment

The “tau topology” on the fundamental group

Posted on November 9, 2024 by Jeremy Brazas

In the multipart series on topologies on fundamental groups, we’ve discussed the fundamental group with the quotient topology: \pi_{1}^{qtop}(X,x_0). This is defined as having the quotient topology with respect to the map q:\Omega(X,x_0)\to \pi_{1}(X,x_0), q(\alpha)=[\alpha] that identifies homotopic loops. Here, \Omega(X,x_0) is the space of loops S^1\to X based at x_0 with the compact-open topology. While \pi_{1}^{qtop}(X,x_0) is a quasitopological group, it often fails to be a topological group.

Here, we’ll finally construct the “tau topology” which is the topological group “fix” to the quotient topology construction. This is, in a sense, dual to the “fix” in which one uses a coreflection functor to push the quotient topology into a Cartesian closed subcategory of spaces, e.g. group objects in k-spaces. Rather, we employ a reflection functor that the forces the quotient topology construction directly into category of topological groups. What is rather remarkable (to me) is that many of the main computational theorems about fundamental groups have analogues in the topological group category.

The universal property of quotient maps implies that \pi_{1}^{qtop}(X,x_0) has the finest topology on the fundamental group such that the map q:\Omega(X,x_0)\to \pi_{1}(X,x_0) is continuous. Why would we want q to be continuous? Well the topology on the fundamental group should remember something about the geometry of representing loops. For instance, if q is continuous, then whenever a sequence of loops \{\alpha_n\}_{n\geq 1} converges uniformly to a loop \alpha, then we might desire this convergence of maps implies the that the sequence of corresponding homotopy classes \{[\alpha_n]\}_{n\geq 1} converges to [\alpha] in the fundamental group. When we make a topology finer, we make it easier to distinguish points using open sets. That \pi_{1}^{qtop}(X,x_0) has the finest topology on \pi_1 with q quotient means that we have maximized our ability to distinguish fundamental group elements topologically while retaining the geometric information provided via q.

In the past two posts (Part I and Part II), I’ve written about the topological group reflection functor \tau that takes in a group with topology G and outputs a topological group \tau(G) with the same underlying group as G by removing the fewest number of open sets from the topology of G until a topological group is obtained. This construction has the following universal property: the identity homomorphism G\to \tau(G) is continuous and if H is a topological group and f:G\to H is a continuous group homomorphism, then f:\tau(G)\to H is continuous. The main idea is to apply this universal construction to the quasitopological group \pi_{1}^{qtop}(X,x_0).

Definition: Let \pi_{1}^{\tau}(X,x_0) denote the topological group \tau(\pi_{1}^{qtop}(X,x_0)). We refer to the topology of this group as the \tau-topology (read “tau-topology”) on the fundamental group.

Since \pi_{1}^{qtop}:\mathbf{Top_{\ast}}\to \mathbf{qTopGrp} and \tau:\mathbf{qTopGrp}\to \mathbf{TopGrp} are both functors (here we restrict the domain of \tau to the full subcategory of quasitopological groups), the composition \pi_{1}^{\tau}=\tau\circ \pi_{1}^{qtop}:\mathbf{Top_{\ast}}\to \mathbf{TopGrp} is a functor. If I had to choose a construction to call the “topological fundamental group” of a space, it’d be this one.

Lemma 1: The function q:\Omega(X,x_0)\to \pi_{1}^{\tau}(X,x_0) that identifies homotopy classes of loops is continuous.

Proof. Since q:\Omega(X,x_0)\to \pi_{1}^{qtop}(X,x_0) is continuous and the identity function \pi_{1}^{qtop}(X,x_0)\to \tau(\pi_{1}^{qtop}(X,x_0))=\pi_{1}^{\tau}(X,x_0) is continuous. The composition of these two maps is the map in the lemma. \square

Theorem 2: The \tau-topology is the finest topology on \pi_1(X,x_0) such that

  1. \pi_1(X,x_0) is becomes a topological group,
  2. q:\Omega(X,x_0)\to \pi_{1}(X,x_0) is continuous.

Proof. By construction, \pi_{1}^{\tau}(X,x_0) is a topological group and 2. was verified in Lemma 1. Let G denote \pi_1(X,x_0) equipped with some topology such that G is a topological group and q:\Omega(X,x_0)\to G is continuous. Since q:\Omega(X,x_0)\to \pi_{1}^{qtop}(X,x_0) is quotient, the universal property of quotient maps gives that the identity function id:\pi_{1}^{qtop}(X,x_0)\to G is continuous. Since G is a topological group, the universal property of the \tau-construction gives that the reflection id:\tau(\pi_{1}^{qtop}(X,x_0))\to G is continuous. Thus \tau(\pi_{1}^{qtop}(X,x_0))=\pi_{1}^{\tau}(X,x_0) has a finer topology than G. \square

Is the \tau-topology really different that the quotient topology? Theorem 2 implies the following. 

Corollary 3: \pi_{1}^{qtop}(X,x_0) is a topological group if and only if \pi_{1}^{qtop}(X,x_0)= \pi_{1}^{\tau}(X,x_0).

Hence, whenever \pi_{1}^{qtop}(X,x_0) fails to be a topological group (and this is often), then the two cannot be the same.

Example 4: In a previous post about the quotient topology, we showed that if \mathbb{E} is the infinite earring space, then \pi_{1}^{qtop}(\mathbb{E},b_0) fails to be a topological group. Hence, \pi_{1}^{\tau}(\mathbb{E},b_0) has a strictly coarser topology than that of \pi_{1}^{qtop}(\mathbb{E},b_0). Exactly which sets are open in \pi_{1}^{qtop}(\mathbb{E},b_0) but not in \pi_{1}^{qtop}(\mathbb{E},b_0) remains very much a mystery. The difficulty here is because the construction G\mapsto \tau(G) is carried out through transfinite recursion and it’s not clear at all how large of an ordinal is required until the recursion stabilizes.

From Example 4, we might be worried that there is no way to understand anything about the \tau-topology. However, the fact that \pi_{1}^{qtop}(X,x_0) is a quasitopological group (has continuous left and right translations and continuous inversion) and not an arbitrary group with topology, provides some help.

Lemma 5 [1, Cor. 3.9]: If G is a quasitopological group and H\leq G, then H is open in G if and only if H is open in \tau(G).

Hence, when we delete open sets from the quotient topology of \pi_{1}^{qtop}(X,x_0) in order to construct \pi_{1}^{\tau}(X,x_0), we never delete any subgroups. Also, from generalized covering space theory (see Part IV) the open (normal) subgroups of \pi_{1}^{qtop}(X,x_0) classify the semicoverings (coverings) of X for all locally path-connected spaces. We have the same Galois correspondences for the \tau-topology $ as well:

\{\text{open subgroups of }\pi_{1}^{\tau}(X,x_0) \}\leftrightarrow \{\text{semicovering maps over }X\}

\{\text{open normal subgroups of }\pi_{1}^{\tau}(X,x_0)\}\leftrightarrow \{\text{covering maps over }X\}

So while we might lose some information when passing from the quotient topology to the \tau-topology we won’t lose a ton of information. In particular, we’ll never lose these covering-map type classifications. 

Those curious enough for more might take a look at my initial paper on the construction or the proof of a topological Nielsen-Schreier theorem [2], which says that every open subgroup of a free topological group is also a free topological group. This is a theorem that filled a long-standing gap in general topological group theory. The only known proof uses topological group fundamental groups, specifically the \tau-topology$. I haven’t done much with the tau-topology in a while but there are several related open questions and unfinished ideas out there.

Topological Analogues of Classical Theorems

The proofs of the following are way too technical for a blog post. So I’ll just share some results that have always surprised me a bit. They serve as evidence that the \tau-topology is probably the most natural extension of the fundamental group to the category of topological groups. All of these are proved in [1].

Classical Theorem A (fundamental group of a wedge of circles is a free group): Let X be a discrete set and X_+=X\cup\{\ast\} be the space with one additional isolated basepoint. If \Sigma X_+ is the reduced suspension (which is a wedge of circles indexed by X), then there is a canonical isomorphism F(X)\to \pi_1(\Sigma X_+) from the free group on the set X.

Topological Theorem A (topological fundamental group of a generalized wedge of circles is a free topological group): Let X be any space and X_+=X\cup\{\ast\} be the space with an additional isolated basepoint. If \Sigma X_+ is the reduced suspension (which is a generalized wedge of circles paramterized by X), then there is a canonical topological group isomorphism F_{M}(\pi_0(X))\to \pi_{1}^{\tau}(\Sigma X_+) from the free Markov topological group on the quotient space \pi_0(X) of path-components of X.

Classical Theorem B: Every group is isomorphic to the fundamental group \pi_1(X,x_0) of some space X obtained by attaching 2-cells to a wedge of circles.

Topological Theorem B: Every topological group is isomorphic to the topological fundamental group \pi_{1}^{\tau}(X,x_0) of some space X obtained by attaching 2-cells to a generalized wedge of circles (see Theorem A).

van Kampen Theorem: If X=U\cup V where U,V,U\cap V are path connected, then there is a canonical isomorphism \pi_1(X)\to \pi_1(U)\ast_{\pi_1(U\cap V)}\pi_1(V) to the pushout in the category of groups.

Topological van Kampen Theorem: If X=U\cup V where U,V,U\cap V are path connected and U\cap V is locally path-connected (or a slightly weaker condition), then there is a canonical isomorphism \pi_{1}^{\tau}(X)\to \pi_{1}^{\tau}(U)\ast_{\pi_{1}^{\tau}(U\cap V)}\pi_{1}^{\tau}(V) to the pushout in the category of topological groups.

References.

[1] J. Brazas, The fundamental group as a topological group, Topology Appl. 160 (2013) 170-188. Open Access.

[2] J. Brazas, Open subgroups of free topological groups, Fundamenta Mathematicae 226 (2014) 17-40.

The \tau-topology was extended to the set of path-homotopy classes of paths starting at a point (the usual universal covering space construction) in the following paper.

[3] Z. Virk, A. Zastrow, A new topology on the universal path space. Topology Appl. 231 (2017) 186-196.

Posted in Category Theory, coreflection functor, Fundamental group, Quasitopological groups, quasitopological groups, quotient topology, reflection functor, topological fundamental group, Topological groups, Uncategorized | Tagged , , , , , , | 1 Comment

Topological Group Reflections: turning a group with topology into a topological group, Part II

Posted on November 6, 2024 by Jeremy Brazas

In Part I, we discussed the operation G\mapsto \tau(G), which takes in a group equipped with a topology (that does not necessarily interact nicely with the operations of the group) and outputs a topological group. The underlying group of \tau(G) is the same as G but the topology of \tau(G) is coarser than that of G. The construction ensures that \tau(G)=G if and only if G is a topological group.

In this post we’re going to show that \tau is a functor and consider the consequences of this fact. Before that recall the inductive construction of \tau(G) requires a step-construction G\mapsto c(G) where c(G) is G equipped with the quotient topology inherited by the map \sigma:G\times G\to G, \sigma(a,b)=ab^{-1}. Using this, we start with G with topology \mathcal{T}_0(G) and recursively define c^{\alpha+1}(G)=c(c^{\alpha}(C)) for each ordinal \alpha and let \mathcal{T}_{\alpha+1}(G) denote the topology of c^{\alpha+1}(G). If \alpha is a limit ordinal then c^{\alpha}(G) is the group G equipped with the topology \mathcal{T}_{\alpha}(G)= \bigcap_{\beta<\alpha}\mathcal{T}_{\beta}(G).

The main idea of the construction is that for any given group with topology G, the transfinite sequence \{c^{\alpha}(G)\}_{\alpha} of groups with topology eventually stabilizes at a topological group \tau(G).

We consider two categories. Let \mathbf{GrpwTop} will denote the category of groups with topology and where the morphisms are continuous group homomorphisms. Let \mathbf{TopGrp} denote the category of topological groups and continuous homomorphisms. Note that \mathbf{TopGrp} is a full subcategory of \mathbf{GrpwTop} and so we have an inclusion functor i: \mathbf{TopGrp}\to \mathbf{GrpwTop}.

Lemma 1: c:\mathbf{GrpwTop}\to \mathbf{GrpwTop} is a functor.

Proof. We have already defined c on objects. Let f:G\to H be a continuous group homomorphism. We define c(f):c(G)\to c(H) to be the same function f. Once we show that c(f) is continuous, the conditions of being a functor follow easily. Recall that \sigma_G:G\times G\to c(G), \sigma_G(a,b)=ab^{-1} and \sigma_H:H\times H\to c(H), \sigma_H(x,y)=xy^{-1} are quotient maps by definition. We have

c(f)\circ \sigma_{G}(a,b)=f(ab^{-1})=f(a)f(b)^{-1}= \sigma_{H}\circ (f\times f)(a,b)

and thus c(f)\circ \sigma_{G}= \sigma_{H}\circ (f\times f).

Commutative diagram with multiplication in vertical arrows and the map f in horizontal arrows.

Since this composition is continuous and \sigma_G is quotient, the map c(f) is continuous by the universal property of quotient maps. \square

Theorem 2: For every ordinal \alpha, c^{\alpha}:\mathbf{GrpwTop}\to \mathbf{GrpwTop} is a functor when we define c^{\alpha}(f):c^{\alpha}(G)\to c^{\alpha}(H) to be the homomorphism f on underlying groups.

Proof. This proof is by transfinite induction. Lemma 1 shows that c^1 is a functor and if c^{\alpha} is a functor, then so is c^{\alpha+1}=c\circ c^{\alpha}. Thus it suffices to focus on the limit ordinal case and show that c^{\alpha}(f) is continuous when \alpha is a limit ordinal. Our induction hypothesis is that c^{\beta} is a functor for all \beta<\alpha. Thus c^{\beta}(f):c^{\beta}(G)\to c^{\beta}(H) is continuous for all \beta<\alpha. To show that c^{\alpha}(f):c^{\alpha}(G)\to c^{\alpha}(H) is continuous, let U\in \mathcal{T}_{\alpha}(H)=\bigcap_{\beta<\alpha}\mathcal{T}_{\beta}(H). For fixed \beta<\alpha, we have U\in \mathcal{T}_{\beta}(H) and since c^{\beta}(f) is continuous, f^{-1}(U)=(c^{\beta}(f))^{-1}(U)\in \mathcal{T}_{\beta}(G). Thus f^{-1}(U)=(c^{\alpha}(f))^{-1}(U)\in \mathcal{T}_{\alpha}(G). We conclude that c^{\alpha}(f) is continuous. \square.

Theorem 3: \tau:\mathbf{GrpwTop}\to \mathbf{TopGrp} is a functor when we define \tau(f):\tau(G)\to \tau(H) to be the homomorphism f:G\to H on underlying groups.

Proof. We have already defined \tau on objects (see Part I for details). Let f:G\to H be a continuous homomorphism of groups with topology. Find ordinals \alpha and \beta with c^{\alpha}(G)=\tau(G) and c^{\beta}(H)=\tau(H). Set \gamma=\max\{\alpha,\beta\}. Then c^{\gamma}(G)=\tau(G) and c^{\gamma}(H)=\tau(H). Since c^{\gamma} is a functor by Theorem 2, we conclude that c^{\gamma(f)}=\tau(f) is continuous. \square.

Using functorality, we can easily verify the “universal property” of the construction \tau(G).

Theorem 4: If G is a group with topology, H is a topological group and f:G\to H is a continuous group homomorphism, then f:\tau(G)\to H is also continuous.

Proof. Recall that the topology of \tau(G) is coarser than that of G so this is not completely obvious. However, we do know that \tau(H)=H is H is assumed to be a topological group. Therefore, applying the functor \tau to f, we have f=\tau(f):\tau(G)\to \tau(H)=H is continuous. \square.

Corollary 5: The topology of \tau(G) is the finest topology on the underlying group of G, which is (1) coarser than that of G and (2) is a group topology (makes the group operations continuous).

Proof. Suppose H denotes the group G with a topology that is (1) coarser than that of G and (2) a group topology. (2) implies that the identity function id: G\to H is continuous. Using (1), we may apply Theorem 4, which implies that id:\tau(G)\to H is continuous. Thus that topology of \tau(G) is finer than that of H. \square.

Conclusion

Theorem 4 implies that \tau:\mathbf{GrpwTop}\to\mathbf{TopGrp} is a reflection functor in the sense that it is left adjoint to the inclusion functor i:\mathbf{TopGrp}\to\mathbf{GrpwTop}. That is, for a topological group latex H and group with topology G, there is a natural bijection \mathbf{TopGrp}(\tau(G),H)\cong\mathbf{GrpwTop}(G,i(H)) that is the identity on homomorphisms of the underlying groups.

This provides a sense in which the construction G\mapsto \tau(G) becomes the most efficient way one can turn a group with topology G (including quasitopological groups). If G is not a topological group and \mu is group multiplcation, then there is some open set U where \mu^{-1}(U) is not open in G\times G. This construction tells us to throw that set U away. Keep throwing away problematic open sets like this until one ends up with only open sets U where \mu^{-1}(U) is open. We had to use transfinite induction to show that such a procedure is possible. That it worked out shows that it is indeed possible to “remove” a smallest number of open sets from the topology of G until a topological group is obtained.

Posted in Categorical Topology, Category Theory, General topology, quasitopological groups, quotient topology, reflection functor, Topological groups, Uncategorized | Tagged , , , , , , , | 3 Comments