One of the infinite abelian groups that is important to infinite abelian group theory and which has shown up naturally in previous posts on infinitary fundamental groups is the Baer-Specker group, often just called the Specker group. This post isn’t all that topological, but I think it’s appropriate considering that infinite group theory is becoming increasingly important to this kind of infinite product-driven algebraic topology.
The Baer-Specker group is the countably infinite direct product of copies of the additive group of integers:
The elements* of the Specker group are sequences of integers
and addition is component-wise
.
We’ll write for the sequence whose only non-zero component is a
in the n-th position. The countable set
forms a basis for the free abelian subgroup
consisting of the sequences
that terminate in
‘s.
But the Specker group is uncountable (as is any countably infinite product of sets with cardinality
), which means the set
cannot generate the whole group – equivalently
is proper.
So is a free abelian group or not?
On the face of it, the answer is not obvious. We answered the same question (with a negative answer) for the earring group in a two-part post (Part I and Part II). This question about the Specker group is a bit easier since it is an abelian group with simpler combinatorial structure. In this post, I’ll walk through a nice, direct proof of the following theorem.
Theorem 1: is not a free group.
You’ll notice the argument is similar in spirit to the argument used to show is not free: basically, we’ll assume the group is free and exploit the infinite structure to find an integer which has infinitely many divisors – something which obviously can’t happen.
*It is also common to view the Specker group as the group 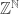 of functions
of functions  from the natural numbers to integers.
from the natural numbers to integers.
History
Apparently, Reinhold Baer [1] first proved Theorem 1 in 1937 (or at least stronger results that imply it). Ernst Specker [3] re-proved this result among a number of other original results about . So the foundational theory of
is often attributed to Specker as well. The proof I’m using in this post is a nice one from the AMM [2].
Free abelian groups and divisibility
First, let’s review some terminology.
Recall that a basis for an abelian group is a subset
such that every element
can be written uniquely as a linear combination
where
for all but finitely many
. An abelian group
is free if such a basis exists.
We will use the following elementary fact about free abelian groups.
Lemma 2: Suppose is a free abelian group with basis
,
is a subset, and
is the free subgroup generated with basis
. The quotient
is a free abelian group for which the set of cosets
form a basis.
Also, we’ll deal with some divisibility issues.
If is an abelian group,
a non-zero element, then we say a natural number
divides
if
for some . We call
a divisor of
and will be interested in cases when an element has finitely or infinitely many divisors. For example, every integer
obviously has only finitely many divisors (using prime decomposition) but every non-zero rational number
has infinitely many divisors since
for every
.
Lemma 3: Every non-zero element of a free abelian group has only finitely many divisors.
Proof. Suppose is a free abelian group with basis
and
is non-zero. Write
uniquely using the basis. Fix some non-zero coefficient
such that
. Notice that if
divides
, then
for some
. But this means
is equal to both
and
.
By the uniqueness of the representation of in the given basis
is equal to
for some
.
We have just argued that whenever divides
, then
also divides the integer
. Since integers only have finitely many divisors,
can only have finitely many divisors.
The Specker group is not free
Proof of Theorem 1. Suppose is a free abelian group with basis
. Since
is uncountable, the indexing set
must also be uncountable.
Write each element as a finite linear combination
of basis elements. For fixed
, let
so that
is the set of indices
which has non-zero coefficient for some element
. Notice that
is countable since it is the countable union of finite sets
. This means the free abelian subgroup
generated by the basis
is also countable.
Remark: It is worthwhile to point out that we have constructed to be the smallest free subgroup (generated by our basis) containing all of the sequences
.
Here are a few important observations:
since
for each
.
- Since
is uncountable, the complement
is also uncountable. Therefore the quotient group
is uncountable.
- By Lemma 2,
is a free abelian group with basis
.
Definition: Let’s say a sequence is multiplicative if for each
, each quotient
of consecutive terms is an integer not equal to
(automatically this means
for any
). Let
be the set of multiplicative sequences.
For example, and
are multiplicative. Let’s quickly convince ourselves that there are uncountably many multiplicative sequences.
Lemma 4: There are uncountably many multiplicative sequences in .
Proof. Consider the set of sequences . Obviously this set is uncountable since, for instance, it contains the uncountable subset
. Define a function
by
. Clearly
is an injection and since
has an uncountable subset,
must be uncountable.
Since is uncountable and
is countable, there exists some multiplicative sequence
such that
.
Recall that and so we have
for each
.
Since is multiplicative, the element
,
where the first non-zero term is in the n+1-st position, is a well-defined element of the Specker group. Notice that
So in the free abelian group , we have
for all
showing that
has infinitely many divisors
in
. But according to Lemma 3, this cannot happen in a free abelian group so we obtain a contradiction.
This concludes the proof that is not free.
How is all this related to the earring group?
In an earlier post, I wrote up a proof of the fact that was not a free (non-abelian) group. The argument was similar the one above for the Specker group but was a bit more sophisticated. Actually, we proved a stronger fact:
Let be the homotopy class of the loop
which traverses the n-th circle of the earring space once in the counterclockwise direction.
Fact: The homomorphism to the Specker group given by
is injective and has image
.
Neither identifying the image of nor proving injectivity of
is easy business. See this post if you’re looking for the proof.
Viewing as the infinite wedge
of circles as a subspace of the infinite torus
, the inclusion map
induces the surjective homomorphism
to the Specker group. Another way to think about this map is that the n-th component of
is the winding number of
around the n-th circle. For example,
and
.
In a similar way, let’s define a homomorphism
, by
and prove the analogous theorem.
Theorem 5: The homomorphism given by
is injective and has image
. Consequently,
is countable.
Proof. Since for each
, the following diagram commutes:
Since is surjective,
is injective. Since both
and
are injective, so is
. Also
(since the triangle commutes). For each
, let
,
be the projection onto the n-th coordinate. Then
showing that
.
Theorem 5 implies Theorem 1: The fact that is countable gives another proof that the Specker group is not free since if it the Specker group is free with (necessarily uncountable) basis
, then the group
of all functions is uncountable.
This viewpoint using the earring group should not be considered an easier proof of Theorem 1 since the hard work is still present on the non-abelian side. On the other hand, exploring the relationship between the two “non-freeness” results – namely that the non-abelian version implies the abelian one – is worth looking at.
References.
[1] R. Baer, Abelian groups without elements of finite order, Duke Math. J. 3 (1937) 68-122.
[2] S. Schroer, Baer’s Result: The infinite product of the integers has no basis, The American Mathematical Monthly 115, No. 7 (2008), 660-663.
[3] E. Specker, Additive Gruppen von Folgen ganzer Zahlen, Port. Math. 9 (1949) 131-140.


Pingback: Celebrating the Career and Contributions of Katsuya Eda: Master of the Hawaiian Earring | Wild Topology
Pingback: Higher Dimensional Hawaiian Earrings | Wild Topology
Nice exposition. One typo in the proof of nonfreeness: You say H has finitely many cosets, but I think you mean finitely many elements.
LikeLike
Right. Thanks!
LikeLike
You may enjoy the fact that the Specker group contains a continuum P_a, for real a \in [0,1], of non-isomorphic subgroups. See
MR0645925 Irwin, John ; Snabb, Tom . A new class of subgroups of Πℵ0Z.
Abelian group theory (Oberwolfach, 1981),
pp. 154–160, Lecture Notes in Math., 874, Springer, Berlin-New York, 1981.
LikeLike
Thanks for sharing Bob! I do really like the way that family of subgroup is defined.
LikeLike
Pingback: Infinite Commutativity: Part I | Wild Topology
Today’s number one hit for google search: Baer Specker not free. Grateful for the helpful walk through.
LikeLike